《线性代数》期终试卷3
![]()
( 3学时)
一、填空题 (15’) :
1
.
设
向量组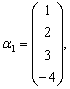

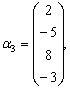
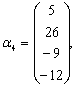
 ,
它的秩是(
)
,一个最大线性无关组是
(
).
,
它的秩是(
)
,一个最大线性无关组是
(
).
2
.
已知矩阵
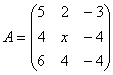 和
和
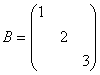 相似
,
则
x
= (
).
相似
,
则
x
= (
).
3
.
设
![]() 是秩为
是秩为
![]() 的
的
![]() 矩阵
,
矩阵
,
![]() 是
是
![]() 矩阵
,
且
矩阵
,
且
![]() , 则
, 则
![]() 的秩的取值范围是
(
).
的秩的取值范围是
(
).
二、计算题:
1
.(7’)
计算行列式
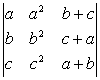 .
.
2
.(8’)
设
 ,
求
,
求
![]() .
.
3
.(10’)
已知
![]() 维向量空间
维向量空间
![]() 的两个基分别为
的两个基分别为
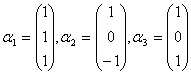 ;
;
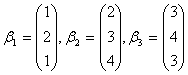 , 向量
, 向量
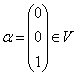 . 求由基
. 求由基
![]() 到基
到基
![]()
![]() 的过渡矩阵
的过渡矩阵
![]() ; 并求向量
; 并求向量
![]() 在这两个基下的坐标.
在这两个基下的坐标.
4
.(15’)
讨论下述线性方程组
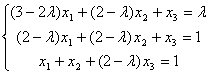 的解的情况;若有无穷多解,则必须求出通解
.
的解的情况;若有无穷多解,则必须求出通解
.
5.(15’
)已知![]()
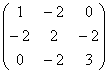 有一个特征值为
有一个特征值为
![]() ,
求正交阵
,
求正交阵![]() ,
使得
,
使得![]() 为对角阵
.
为对角阵
.
6
.(10’)
在次数不超过
3的实系数多项式所成的线性空间
![]() 中定义线性变换
?
为
?
中定义线性变换
?
为
?
![]() =
=
![]() , 求线性变换
?
在基
, 求线性变换
?
在基
![]()
下的矩阵
![]() .
.
三、证明题:
1.
(10’)
已知矩阵
![]() 与
与
![]() 合同,
矩阵
合同,
矩阵![]() 与
与
![]() 合同,
证明:
分块对角矩阵
合同,
证明:
分块对角矩阵
![]() 与
与
![]() 也
合同
.
也
合同
.
2
.(10’)
设
![]() 是正交
矩阵
,
是正交
矩阵
,
![]() ,
,
![]() 是
是
![]() 的特征值
,
的特征值
,
![]() 是相应于特征值
是相应于特征值
![]() ,
,
![]() 的特征向量
,
问
:
的特征向量
,
问
:
![]() 与
与
![]() 是否线性相关
,
为什么
?
是否线性相关
,
为什么
?
![]() 与
与
![]() 是否正交
,
为什么
?
是否正交
,
为什么
?