《线性代数》期终试卷4
![]()
( 3学时)
本试卷共九大题
一、 选择题(本大题共 4个小题,每小题2分, 满分 8分):
1.
若![]() 阶方阵
阶方阵![]() 均可逆,
均可逆,![]() ,则
,则![]()
(A)
![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]() 答(
)
答(
)
2.
设![]() 是
是![]() 元齐次线性方程组
元齐次线性方程组
![]() 的解空间,其中
的解空间,其中
![]() ,则
,则![]() 的维数为
的维数为
(A)
![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]() 答(
)
答(
)
3.
设![]() 是
是![]() 维列向量,则
维列向量,则
![]() =
=
(A)
![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]() 答(
)
答(
)
4.
若向量组![]() 可由另一向量组
可由另一向量组
![]() 线性表示,则
线性表示,则
(A)
![]() ;
(B)
;
(B)
![]() ;
;
(C)
![]() 的秩
的秩![]()
![]() 的秩;(D)
的秩;(D)
![]() 的秩
的秩![]()
![]() 的秩.
的秩.
答( )
二、 填空题( 本大题共 4个小题,每小题3分, 满分12 分):
1.
若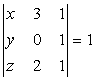 ,则
,则 。
。
2.
设![]() ,
,![]() ,
,![]() ,则
,则![]()

3.
设4
阶方阵![]() 的秩为2
,则其伴随阵
的秩为2
,则其伴随阵
![]() 的秩为
。
的秩为
。
4.
设![]() 是方阵
是方阵![]() 的一个特征值,则矩阵
的一个特征值,则矩阵
![]() 的一个特征值是
。
的一个特征值是
。
三、计算行列式
 ,(
,(![]() )
)
(满分8 分)
四、
设![]() ,
,![]()
 ,
,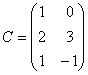 ,求
,求![]() ,使得
,使得![]() 。
。
(满分12 分)
五、
在
![]() 中有两组基:
中有两组基:
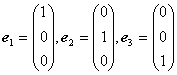 和
和
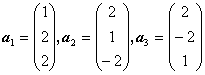
写出
![]() 到
到![]() 的变换公式以及
的变换公式以及![]() 到
到![]() 的变换公式。
的变换公式。
(满分8 分)
六、
当![]() 取何值时,线性方程组
取何值时,线性方程组

有唯一解、无解或有无穷多解?并在有无穷多解时求出通解。
(满分14 分)
七、
已知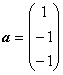 ,
,![]() 为3
阶单位矩阵,
为3
阶单位矩阵,
![]() ,求一个正交矩阵
,求一个正交矩阵
![]() ,使得
,使得![]() 为对角阵,并写出该对角阵
.
为对角阵,并写出该对角阵
.
(满分16 分)
八、
设![]() 为已知的
为已知的![]() 矩阵,集合
矩阵,集合
![]()
1.
验证![]() 对通常矩阵的加法和数乘构成实数域
对通常矩阵的加法和数乘构成实数域
![]() 下的线性空间;
下的线性空间;
2.
当![]() 时,求该线性空间的一组基。
时,求该线性空间的一组基。
(满分10 分)
九、 证明题( 本大题共 2个小题,每小题6分, 满分 12分 ):
1.
设![]() 为一向量组,其中
为一向量组,其中
![]() 线性相关,
线性相关,
![]() 线性无关,证明
线性无关,证明
![]() 能由
能由![]() 线性表示。
线性表示。
2.
若![]() 为
为![]() 阶方阵,
阶方阵,![]() ,证明:
,证明:![]() 为可逆矩阵。
为可逆矩阵。